Behind The Algorithm #4 - 👨🏻‍💻 How to design an Algorithm? | ghack.dev

Have you ever seen a very beautiful building with its complexity?

Like this for example:

There should be a way, a method, a technique, or a step-by-step to design that beautiful building. Also, there should be a way to measure the balance or the strength, or any other metrics before the architect could bring the plan on the sketches into a real building.

Because sometimes, good is not enough to build a very complex, solid, and also beautiful building. The architect needs to master some skills, knowledge, and a lot of experiences to create a design, which is not only beautiful but also design should be possible to be translated into a real building.

In our case, the building is an Algorithm

Unconsciously, we already analyzed one of these techniques that I want to introduce to you.

Incremental approach

Incremental approach is as what we did when implementing the Insertion sort:

We have sorted subarray a[1...j-1].
Inserted single element a[j] to its proper place in the subarray.
As a result we have sorted array a[1...j].

As we know that the time complexity for insertion sort is quite bad which is $O(n^2)$ for the worst case. In this article, we will learn another design approach that is better than the design approach we used on insertion sort.

Divide-and-conquer approach

The main idea of this approach is to divide the problem into chunks, conquer / solve the problem on each of the chunks one by one, and then combine the result of each chunk to return the root to create a solution to the original problem. It sounds pretty simple, right?

Some of the famous algorithms out there are using the recursive structure. It means that the function will call itself recursively to deal with closely related sub-problems.

Merge sort

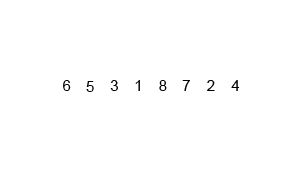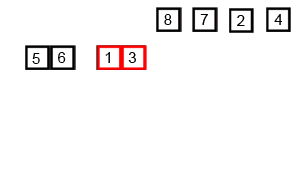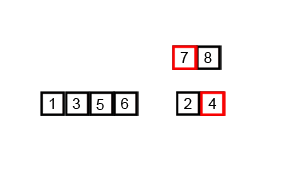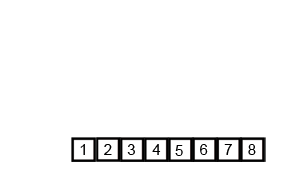
Source: https://en.wikipedia.org/wiki/Merge_sort#/media/File:Merge-sort-example-300px.gif

Merge sort is designed using the divide-and-conquer approach. That's why the step-by-step of this sorting algorithm is, let say the input would be an array of number with the length $n$ :

Divide the input into two sub-array with length $(n / 2)$ for each of them.
Conquer that two sub-arrays by recursively calling the merge sort function.
Combine that two sorted sub-array to produce the whole sorted answer.

Let's jump to the code...

In our Merge sort implementation on pseudo-code, we will have two functions. The first function is the merge function and the second function is the main function named merge_sort.

Let's go to the first function called merge.

1. FUNCTION merge(arr_a, arr_b)
2.    i = 0
3.    j = 0
4.
5.    result = []
6.
7.    WHILE TRUE:
8.        a = NONE
9.        b = NONE
10.
11.       IF i <= arr_a.LENGTH - 1
12.           a = arr_a[i]
13.       IF j <= arr_b.LENGTH - 1
14.           b = arr_b[j]
15.
16.       IF a == NONE AND b == NONE
17.           BREAK
18.       ELSE IF a == NONE AND b != NONE
19.           result.PUSH(b)
20.           j = j + 1
21.       ELSE IF b == NONE AND a != NONE
22.           result.PUSH(a)
23.           i = i + 1
24.       ELSE IF a < b
25.           result.PUSH(a)
26.           i = i + 1
27.       ELSE
28.           result.PUSH(b)
29.           j = j + 1
30.
31.   RETURN result

I'm sorry, it's quite long but the idea behind this code is pretty simple. Imagine you have two piles of cards and you want to merge those piles into one pile. Let's name the first pile as left pile and the second pile as right pile.

What you do is to open the first card on the left pile -> open the first card on the right pile -> compare the number of between those cards -> take one card with a smaller number and put it into the output pile -> put back the card with the bigger number back to its pile.

Repeat steps above until there's no more card on those two piles, when that happens we already have the full output pile. Pretty simple right? 😊 Let's go to the main function called merge_sort then.

1. FUNCTION merge_sort(arr)
2.    n = arr.LENGTH
3.    half = n / 2
4.
5.    result = []
6.
7.    IF n > 1
8.        arr_left = arr[1...half]
9.        arr_right = arr[half...n]
10.
11.       left = merge_sort(arr_left)
12.       right = merge_sort(arr_right)
13.
14.       result = merge_arr(left, right)
15.   ELSE IF n == 1
16.       RETURN arr
17.
18.   RETURN result

As you can see, it's a very simple function. In line 3 half = n / 2 it will get the middle index of the array by dividing the length by two.

And then if the condition in line 7 IF n > 1 is true, it will divide the array into two subarrays (left and right) for each of the sub-array it will call the merge_sort functions recursively by feeding those subarrays as a parameter.

And after the recursive calling ends, it will merge the left and right array in line 14 result = merge_arr(left, right) and put to the result variable, and then it would simply return the result in line 18 RETURN result.

In another case when the condition in line 7 IF n > 1 is false, it will just return the array from the function parameter directly, in other words, when the length of the array is exactly one, that's the end of the recursive calls.

Let's break down the running time of this Algorithm...

We will not calculate the running time line by line as we did before on the Insertion sort. We will just calculate the running time by looking at it's three main steps.

The Divide step will just divide the length of the array by two and split the array into two subarrays, let's say it will take constant time, which is $O(n)$

The Conquer step will recursively solve two subarrays with length $n/2$ , which is $2T(n/2)$ .

The Combine step will merge the subarrays into a single array and it will take $On$ .

So, if n = 1:
$T(n) = O(1)$

And if n > 1:
$T(n) = 2T(n/2) + cn$

Recursion Tree

We can imagine the merging time for all subproblems of the size $cn$ as a recursion tree.

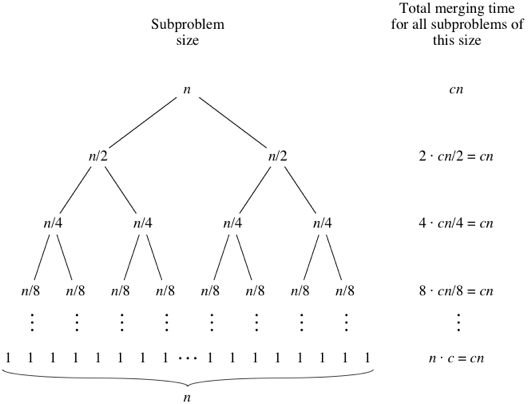
Source: https://cdn.kastatic.org/ka-perseus-images/5fcbebf66560d8fc490de2a0d8a0e5b1d65c5c54.png

The total number of levels of the recursion tree above is excactly $log_2 n + 1$ where $n$ is the number of leaves. Okay, now we understand the the recursion tree has $log_2 n + 1$ levels, the cost of each of them is $cn$ , for a total cost of $cn(log_2 n + 1) = cn . log_2 n + cn$ . We can ignore all of the low-order term and the constant $c$ gives the desired result of $O(n.log_2 n)$ .