Behind The Algorithm #3 - ⏱ Running Time & Time Complexity | ghack.dev

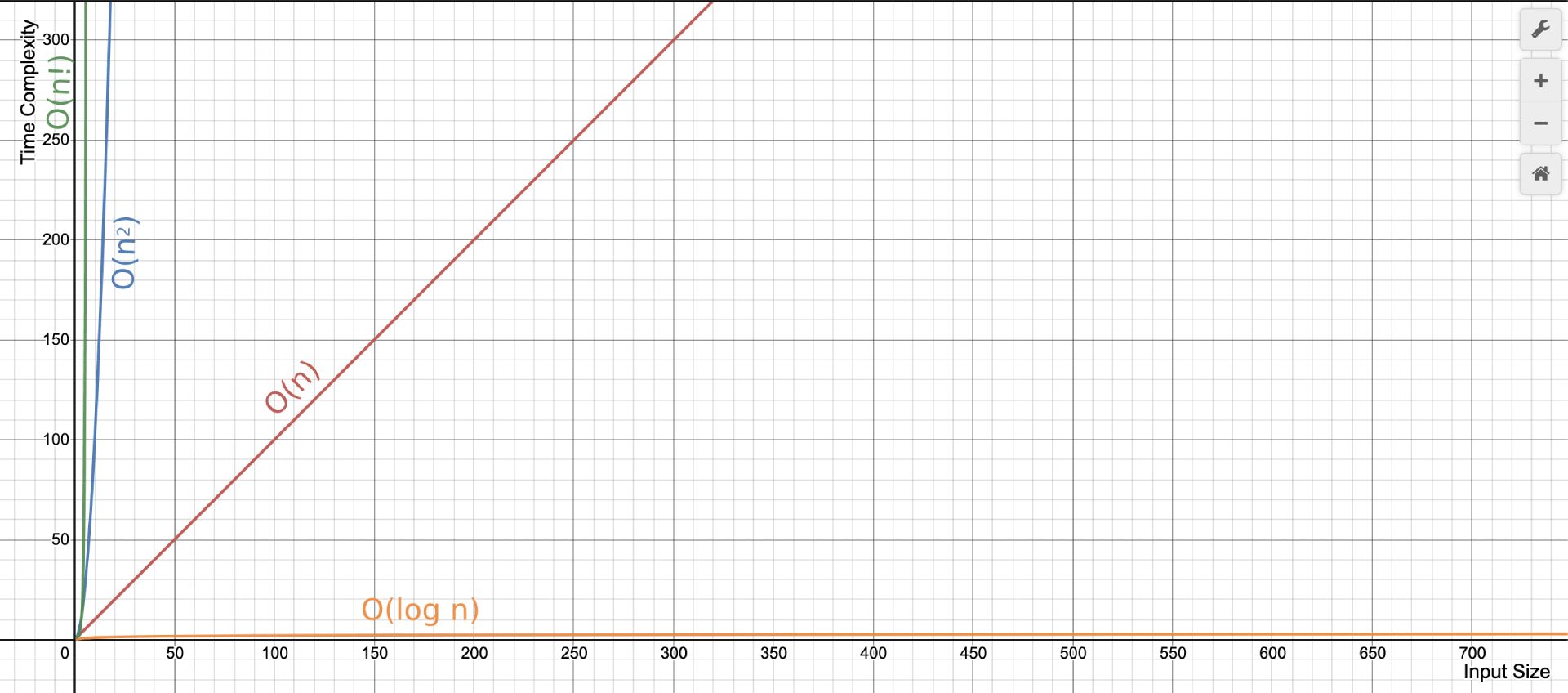
What is Time Complexity?

Simply say, the time complexity is just an amount of time taken by an algorithm to produce an output based on the input size.

As you can see in the image above, the time complexities are expressed as a mathematical notation that usually we call it Big O notation. The time complexity growth varies for each one of them. From the very small growth which is the $O(\mathbf{n})$ until the craziest growth $O(\mathbf{n}!)$ .

How do we use the Big O notation to measure the performance of our Algorithm?

Let's start by analyzing the Big O notation of this very simple algorithm:

numbers = [1,2,3,4,5,6,7,8] // <-- the input

// because it's just a pseudo-code so to access
// first element on the array, we're going to use number 1 instead of 0.

FOR i = 1 TO numbers.LENGTH
    PRINT(numbers[i]) <-- the output

Don't try to run it on any compiler or interpreter because that's only a pseudo-code, my version of pseudo-code. 😬

Code above is only a simple algorithm that takes an array of numbers named numbers as an input and print all of the numbers inside the array inside variable named numbers as an output. Could you determine the time complexity for that Algorithm? Let's measure it together.

// let's just focus on the looping syntax.

FOR i = 1 TO numbers.LENGTH
    PRINT(numbers[i])
    // ^ this line would be excecuted 8 times because
    // the for loop would start at i = 1 and would end until the `i`
    // is equal to the length of the array named `numbers` which is 8.

So the time complexity growth for this code would always equal to the length of the input, The Big O notation for this algorithm is $O(\mathbf{n})$ , or commonly we can call the growth as linear growth. It's very simple, right?

Let's go to the next Algorithm...

n = 4
FOR i = 1 TO n
    line = ""
    FOR j = 1 TO n
        line = line + "*"
    PRINT(line)

It's just another simple algorithm to print a star with $n * n$ dimensions. How's the time complexity? Yes! It's exactly $O(\mathbf{n^2})$ . Is it too easy for you?

Let's go to the more complicated one...

This time, we will try to be more detail and try to measure the running time of one of the famous sorting algorithms named Insertion Sort. This is a very simple sorting algorithm that would be efficient enough to sort a small-sized input.

We can easily understand how this algorithm works by imagining how we sort a hand of cards. This animation can help you understand more easily.

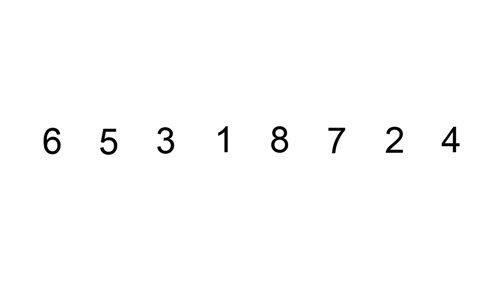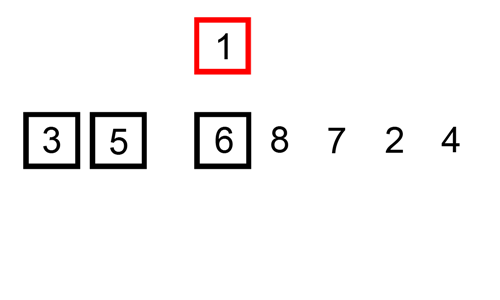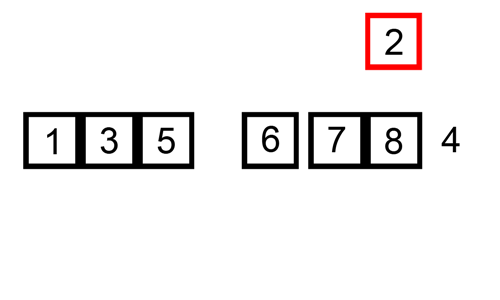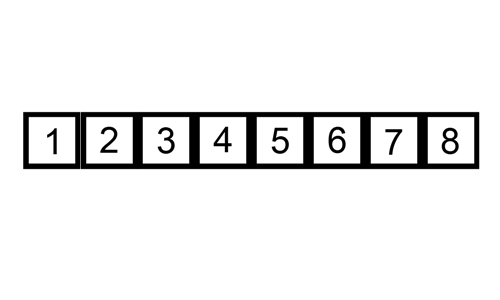
Source: https://upload.wikimedia.org/wikipedia/commons/9/9c/Insertion-sort-example.gif

This is the pseudo-code of the insertion sort:

FUNCTION insertion_sort(a)
1.  FOR i = 2 TO a.LENGTH
2.      number = a[i]
3.
4.      j = i - 1
5.       WHILE j > 0 AND a[j] > number
6.          a[j + 1] = a[j]
7.          j = j - 1
8.       a[j + 1] = number

As I said before that we would be more detailed this time, we will try to calculate the total execution time (running time) of this Insertion Sort algorithm line by line.

`1. FOR i = 2 TO a.LENGTH`	-> $n$
`2. number = a[i]`	-> $(n - 1)$
`4. j = i - 1`	-> $(n - 1)$
`5. WHILE j > 0 AND a[j] > number`	-> $\sum_{(j = 2)}^{n} {t_j}$
`6. a[j + 1] = a[j]`	-> $\sum_{(j = 2)}^{n} {t_j - 1}$
`7. j = j - 1`	-> $\sum_{(j = 2)}^{n} {t_j - 1}$
`8. a[j + 1] = number`	-> $\sum_{(j = 2)}^{n} {t_j - 1}$

In this article, I will be more focused on measuring the algorithm without thinking about the "real cost" when we execute the code on a computer with its hardware, so let's assume the cost of the execution for each line of code is $c_x$ , for $x =$ line of code.

Calculating the best case...

The running time of an algorithm does not only depend on the length of the input, but also the condition of the input itself. In this case, we will try to calculate the best case first. The best-case happens in this case when the input is already sorted.

So, as you can see in line 5, the while loop condition a[j] > number will always false because a[j] <= number. So this is how we calculate the best-case running time mathematically:

\begin{aligned} T(n) & = {c_1(n) + c_2(n - 1) + c_4(n - 1)} \\ & + {c_5(n - 1) + c_8(n - 1)} \\ & = {(c_1 + c_2 + c_4 + c_5 + c_8)n} \\ & - {(c_2 + c_4 + c_5 + c_8)} \end{aligned}

So we can express it simply by writing it like this $an + b$ , it's a linear function of $n$ .

Calculating the worst-case...

The worst-case happens when the input is in reverse order like this [5,4,3,2,1].

\begin{aligned} T(n) & = {c_1(n) + c_2(n - 1) + c_4(n - 1)} \\ & + {c_5(\frac{n(n + 1)}{2} - 1) + c_6(\frac{n(n - 1)}{2})} \\ & + {c_7(\frac{n(n - 1)}{2}) + c_8(n - 1)} \\ & = {(\frac{c_5}{2} + \frac{c_6}{2} + \frac{c_7}{2})n^2} \\ & + {(c_1 + c_2 + c_4 + \frac{c_5}{2} - \frac{c_6}{2} - \frac{c_7}{2} + c_8)n} \\ & - {(c_2 + c_4 + c_5 + c8)} \end{aligned}

So we can express the worst-case running time as $an^2 + bn - c$ . So as you can see it's a quadratic function of $n$ .

Wow, The Insertion Sort just transformed from linear to quadratic for a different case (best -> worst).

Worst-case vs Average-case running time

We have analyzed and calculate the running time of Insertion Sort for the best and worst-case. How about average-case? Hmm, actually, thinking of the average case is not giving us useful information. Rather than thinking about the average case, we should be more concentrated to find the worst-case running-time. Why?

Because...

Worst-case could give us the upper bound for any input, in other words, it's never getting worse than the worst-case for any kind of input.

So, thinking about the best or average case is kind of useless, so we decided to not focus on both of them. ☺

Running Time vs Rate Of Growth

As you can see from the calculation we did above, we know that the total running time for the worst-case is $an^2 + bn - c$ . Actually, that's too much and too detail, so maybe we can ignore the constants a, b, and c which representing the actual cost of the execution of each line.

So we could abstract it as rate of growth. So we can just express the rate of growth as a Big O notation $O(n^2)$ . Remember, that rate of growth is different with running time. The rate of growth is describing how the time complexity grows along with the input.